Центростремительной силы в природе нет
Центростремительной силы в природе нет, также как нет и центростремительного ускорения. Зададим себе вопрос: «Откуда же и когда появилась эта мифическая величина центростремительная сила с не менее мифическим центростремительным ускорением?» Анализируя некоторые публикации о том, что таких понятий как центростремительная сила и центростремительное ускорение в природе нет, не встретил ни одной публикации, в которой бы академическая наука каким-то образом реагировала на подобные публикации и на результаты многочисленных экспериментов, убедительно доказывающих, что центростремительной силы нет, как нет и центростремительного ускорения. В результате решил написать статью, чтобы показать, откуда происходит сама ошибочная идея, и когда впервые появились эти термины «центростремительная сила» и «центростремительное ускорение» в учебниках по физике. Однако, попытка найти первоисточник, в котором впервые появился термин «центростремительная сила» не удалась. Правда есть ссылка в Википедии о том, что термин «центробежная сила» впервые ввел И. Ньютон в 1609 году. Видимо, термин «центростремительная сила» появился спонтанно в противовес центробежной силе, но дата его появления не определена. Пришлось в настоящей статье сделать ссылку на учебник по элементарной физике под редакцией академика Г. С. Ландсберга 1966 года издания.
Следует сразу сказать, что не нужно «путать» термин «центростремительная сила» с силой тяготения и силами деформации. Но сначала напомню еще раз, что говорят на эту тему результаты экспериментов. Рассмотрим три наиболее часто демонстрируемые в разных публикациях эксперименты.
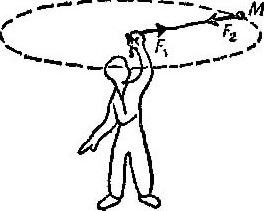
1. Вспомним классический опыт, в котором грузчик вращается на нити по окружности с неподвижной осью вращения в центре окружности. Чем больше скорость вращения грузика, тем сильнее натягивается нить. На первый взгляд действительно кажется, что натяжение нити, говорит о том, что на грузик действует сила, направленная к оси вращения (к центру траектории). Но представим себе, что нить в какой-то момент времени обрывается и куда будет двигаться грузик? Правильно, он будет двигаться в сторону от окружности по касательной к ней, но только не к центру окружности. Спрашивается, где же эта центростремительная сила? Еще раз отметим, что и в этом, и других подобных опытах сила, направленная к центру, представляет собой совокупность сил деформации – силы деформации оси, силы деформации нити и силы деформации самого грузика в месте закрепления нити (Рис.1). В соответствии с 3-им законом И. Ньютона сила деформации возникает из-за действия на нить центробежной силы (силы инерции), действующей на вращающийся грузик, которая равна силе деформации и противоположна ей по направлению.
2.Второй опыт, который иногда в разных модификациях демонстрируют в видеороликах интернета, представляет собой колесо со спицами (Например, велосипедное колесо), на которых закреплены грузики с возможностью свободного перемещения вдоль спиц, Рис.3. Грузики на нескольких спицах расположены на разных расстояниях от центра колеса и, соответственно, от обода колеса. Колесо начинает вращаться и, при определенной скорости вращения колеса, грузики начнут друг за другом двигаться от центра к ободу колеса. Первым начнет двигаться грузик, дальше других отстоящий от центра. При достаточно больших оборотах все грузики окажутся прижатыми к ободу колеса, Рис.4. И чем больше скорость вращения колеса, тем больше давление будет на обод колеса, тем больше будет сила инерции. Ни один из грузиков не будет двигаться к центру колеса в результате действия на грузики не существующей центростремительной силы.
3.Приведу еще один опыт, наглядно демонстрирующий отсутствие центростремительной силы. Это когда грузик закреплен вместо нити на пружине. При вращении вокруг неподвижной оси пружина будет растягиваться, показывая стремление грузика двигаться от центра, от оси. И чем больше будет угловая скорость вращения, тем дальше грузик будет удаляться от оси и, тем больше растягивать пружину. Пружину растягивает центробежная сила (сила инерции), равная и противоположная по направлению силе деформации пружины, которая направлена к центру окружности, к оси закрепления пружины.
Аналогичная картина происходит и при движении трамвая на поворотах рельсовой дороги. При этом, сила инерции вызывает деформацию рельсов и чем больше скорость трамвая, тем больше деформация рельсов и, тем больше сила инерции. Ни в одном из этих опытов мы не наблюдаем действие центростремительной силы. Да и как можно наблюдать то, чего на самом деле нет.
Центробежная сила (сила инерции) равна и противоположна по направлению силе деформации, и пропорциональна скорости движения материального тела по криволинейной траектории. Но если центробежная сила и сила деформации равны и действуют в противоположных направлениях, т. е. ни одна из этих сил не действует на тело в направлении его движения, то что же вызывает движение тела по окружности? Значит, кроме этих двух сил, существует еще одна (третья) сила, которая и вызывает движение тела по окружности, криволинейной траектории. Но об этом в следующей публикации.
Здесь уместно поговорить еще об одном опыте. Представим себе вращающийся на нити грузик в плоскости чистого листа бумаги. В грузике сделано отверстие для того, чтобы вставить шариковую ручку таким образом, чтобы шарик ручки касался листа бумаги. При вращении грузика, на чистом листе бумаги образуется траектория движения грузика, отмеченная шариковой ручкой, Рис.5. Эта траектория является окружностью с центром, совпадающим с осью закрепления нити. Как бы мы не старались, никаких отклонений грузика от круговой траектории в направлении к центру мы не заметим даже в самые малые промежутки времени. А все эти виртуальные векторы скорости являются только чистой фантазией (вымыслом) авторов подобных публикаций и придуманы авторами для того, чтобы «запудрить» мозги школьникам и студентам, начинающим изучать физику.
А теперь постараемся ответить, с моими комментариями, на поставленный в начале настоящей статьи вопрос: «Откуда же появилась эта мифическая величина центростремительная сила с не менее мифическим центростремительным ускорением»?
Так в учебнике под редакцией академика Г. С. Ландсберга по элементарной физике утверждается, что «движение по окружности есть движение с постоянным по величине ускорением, направленным к центру окружности». Откроем этот учебник по физике т.1 с.68-69. Читаем довольно смелое утверждение: «Таким образом, в криволинейном движении всегда имеется изменение скорости, т.е. это движение происходит с ускорением». Замечу, что подобное и другие утверждения далее по тексту, добросовестно копируются, с небольшими изменениями, и другими авторами (любителями жонглировать с векторами) в учебниках по физике. А затем. «Для определения этого ускорения (по величине и направлению) требуется найти изменение скорости как вектора (как это возможно? Особенно это касается изменения величины скорости), т.е. требуется найти изменение величины и изменение направления скорости». Далее, прокомментируем удивительный по логике ход мыслей автора, когда он (автор), приступает к выводу формулы для центростремительного ускорения при движении тела по окружности (см. Рис.6). «Движение точки происходит из положения А в положение В, за промежуток времени t. Скорости точки в А и В равны по величине, но различны по направлению»? Допустим. «Разность этих скоростей находят из подобия равнобедренных треугольников АОВ и А1ВВ1″. (Причем здесь физические величины и геометрические отрезки?) «Длину стороны А1В1, изображающей приращение скорости» (надо же, никакого приращения скорости нет, точка – тело движется по окружности с постоянной скоростью) «за промежуток времени t, можно положить равной ахt, где а- величина искомого ускорения». Приращение скорости, о котором говорит автор есть абсурд. Никакого приращения скорости нет, можно говорить лишь о скорости изменения, и даже не направления виртуального вектора скорости, а о скорости изменения угла между двумя соседними виртуальными векторами. «Сходственная ей сторона АВ есть хорда дуги АВ. Вследствие малости дуги ее хорда может быть приближенно принятой равной длине дуги, т.е. vхt (опять условности). Далее ВА1=ВВ1=v» (как длина отрезка может быть равна величине скорости?). «ОА=ОВ=R, где R-радиус траектории». А далее у автора получается проще простого, «из подобия треугольников следует, что отношения сходственных сторон в них равны: aхt/vхt=v/R, откуда находим искомое ускорение». (Где сапоги, а где пироги?). «Направление ускорения перпендикулярно к хорде АВ», (это почему же?). Оказывается, «для достаточно малых промежутков времени можно считать, что касательная к дуге практически совпадает с ее хордой» (опять натяжка), «значит, найденное (мифическое) ускорение можно считать направленным перпендикулярно к касательной к траектории», (странное утверждение), «т.е. по радиусу к центру окружности. Поэтому такое ускорение называют нормальным или центростремительным ускорением» - удивительное по логике заключение. Ну как вам такой конгломерат? Если есть центростремительное ускорение, значит есть и центростремительная сила, вызывающая это ускорение?
Кроме того, у автора отрезок w на рис.6, являющийся стороной параллелограмма, представлен как ɷ -изменение скорости.
Но, во-первых, это изменение направления виртуального вектора скорости, и к величине скорости не имеет никакого отношения (скорость движения тела по окружности одинакова), а во-вторых, в этом случае, можно говорить только о скорости изменения угла между двумя соседними виртуальными векторами, изображающими направление скорости по касательной к траектории, о чем говорилось выше. Указанный угол равен углу между двумя радиусами, соединяющими точки касания двух соседних виртуальных векторов (что легко доказывается дополнительным геометрическим построением к рис.6), и скорость изменения центрального угла –а- равна скорости изменения угла ε, образованного двумя соседними виртуальными векторами ɷ=ε/t касательными к траектории окружности и скорость этого изменения за время t для обоих углов одинакова и не меняется во время движения точечного тела по окружности с постоянной скоростью и равна V= ɷхR. А ловкое жонглирование виртуальными векторами, «смешивание» физических величин с геометрическими отрезками, приводит к несуществующим в природе понятиям, таким как центростремительная сила и центростремительное ускорение, и вводит начинающих изучать физику в заблуждение. Эти понятия внесены в учебники с давних пор, их авторы добросовестно переписывают упомянутые физические величины из учебника в учебник, и, говоря современным языком (извините), «впаривают» их школьникам и студентам до настоящего времени. Использование этих понятий приводит к искажению физического смысла многих физических явлений при проведении экспериментов и в самой природе. Будем надеяться, что академическая наука в конце концов обратит свое внимание на этот «казус» и внесет изменения в учебниках по физике.
Еще несколько слов о применении 2-го закона И. Ньютона к движению тел по криволинейной траектории. Как применять второй закон И. Ньютона к криволинейному движению и что в этом случае является ускорением? Мы привыкли применять 2-ой закон, не задумываясь над тем, применим ли он для движения тел по криволинейным траекториям? Опыты показывают, что этот закон применим для движения материальных тел по прямой линии, когда тело массой М ускоряется под действием постоянной внешней силы. Например, когда тело падает на Землю, то оно падает с ускорением свободного падения равным 9,8 м/с2 под действием силы тяготения. Все тела падают на Землю с одинаковым ускорением независимо от массы тел. В этом случае тело движется по прямой и 2-ой закон И. Ньютона применим к прямолинейному движению. А криволинейное движение, как определить, что здесь является ускорением? О каком ускорении мы говорим, если скорость движения, например, по окружности постоянна и ее величина не изменяется? На эти и подобные вопросы мне кажется должна ответить академическая наука.
Примечание. Предложения в тексте статьи, отмеченные жирным шрифтом, взяты из оригинала упоминаемого учебника.
Выводы.
1. В статье приведены, часто демонстрируемые в публикациях, опыты, результаты которых подтверждают отсутствие центростремительной силы.
2.Показана несостоятельность вывода, применяемого в учебниках по физике, о существовании центростремительного ускорения.
3.В целом показано, что в природе не существует ни центростремительной силы, ни центростремительного ускорения, ни центробежной силы.
4.Настоящая статья является наглядным примером того, как математика может быть «притянута за уши» для описания несуществующего явления природы.






Здравствуйте, Иван Иванович! Пишет Вам такой же пенсионер увлечённый наукой, как и Вы. Вы совершенно правы — нет никакой центростремительной силы и ускорения. Все орбиты активных небесных тел образованы с момента возникновения Вселенной и образованы микроскопическими, космическими телами — прообразами будущих звёзд и потомков звёзд — планет.